Partial and directional derivatives
Partial and directional derivatives generalizes the concept of derivatives to the context of real-valued functions in several variables.
In this lecture, we start the development of the concept of derivatives for real-valued functions in several variables. Partial and directional derivative are two closely related construction that turns the problem of quantifying the rate of change of a function in several variables into the familiar problem of understanding the rate of change of a function in one variable only.
Review: derivative
Recall that for a function $f$ in one variable, its derivative function is defined to be \[ f'(x) = \lim_{h \to 0} \frac{ f(x+h) - f(x) }{ h } \] wherever this limit exists. It give us a tool to measure how fast a function changes, i.e., the instantaneous rate of change of the function.
We want to generalize this idea to functions in several variables.
As usual, we will use the boldface symbol for ordered list of $n$ variables, i.e., $ \mathbf{x} = (x_1,\dots,x_n), $ whenever we make general statements for any dimension.
Partial derivatives of functions in two variables
For a real-valued function $f$ in two variables, we can gain some understanding of how this function changes its value by looking at the cross sections of the graph of $f$ along the $x$ and $y$ directions separately.
That is, $\frac{\partial f}{\partial x}$ is the derivative of $f$ when $y$ is held constant, and $x$ is considered to be the only variable.
From a geometric point of view, $\frac{\partial f}{\partial x}$ describes the slope of the tangent lines of cross sections of the graph of $z = f(x,y)$ along the $x$ direction.
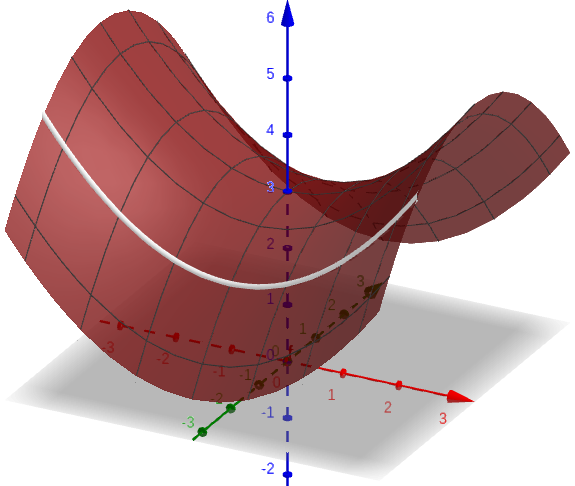
This figure shows a cross section of the graph of $f(x,y) = \frac{x^2-y^2}{5}+3$ with $y$ fixed at $-2$.
For any $x$ value, $\frac{\partial f}{\partial x} (x,-2)$ gives us the slope of the tangent line to this cross section at $(x,-2)$.
In general, fixing any $y$ value, $\frac{\partial f}{\partial x}$ gives us the slopes of the tangent lines to a horizontal cross section.
Basically, $\frac{\partial f}{\partial x}$ gives us a meaningful slope at any point, if we are restricted to move in the $x$ direction only.
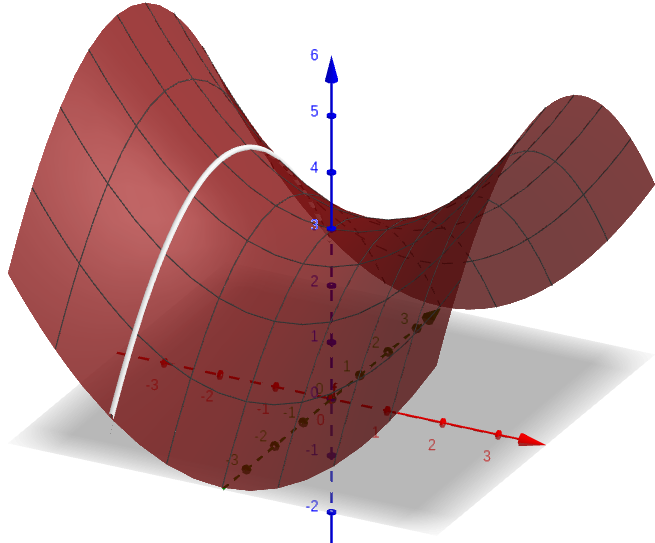
We can define the partial derivative of $f$ with respect $y$ in a similar way.
That is, $\frac{\partial f}{\partial y}$ is the derivative of $f$ when $x$ is held constant, and $y$ is considered to be the only variable.
We have a similar geometric interpretation: $\frac{\partial f}{\partial y}$ gives us the slopes of the tangent lines to cross sections along the $y$ direction.
Exercises
When calculating the partial derivative of a function $f$ with respect to a variable, we simply have to "pretend" all other variables are numbers.
All the familiar differentiation techniques still apply here.
Partial derivative of functions in several variables
What we described can be easily generalized to real-value functions in any number of variables.
This definition agrees with our definitions for the 2-variables cases. If $n=1$, this definition also agrees with the familiar definition of derivatives of functions of a single variable.
Differentiability: the technical definition
It turns out partial derivatives are rather "weak" concepts and not sufficient to capture of idea of derivative and differentiability for functions in several variables. We will develop a stronger concept.
This is an important but rather complicated concept. We will have a separate discussion on its deeper meaning.
For now, we will only take this to mean the condition that the function can be arbitrarily closely approximated by a linear map.
Differentiability is a stronger condition
The concept of differentiability we just defined is a strictly "stronger" condition than the existence of partial derivatives in the sense that being differentiable implies the existence of partial derivatives.
The converse is not true: It is possible for a function to have all the partial derivatives at a point, but the function is not differentiable at that point. We will have a better understanding of these points in a separate discussion.
At this moment, we will simply take "differentiability" as a nice condition under which we can develop other concepts and tools easily.
Chain rule
The familiar chain rule also has a nice generalization to the context of functions of several variables. For simplicity, we start with two variables.
Alternatively, we can also write the above equation more compactly as \[ [ f(x(t),y(t)) ]' = f_x x' + f_y y' \] with the points at which the functions are evaluated being implicit.
The proof is fairly complicated, but if you understood how chain rule works, maybe you can see why this one "has to be" true. Can you give it a try?
Exercises
Slightly more general chain rule
Notice that the right hand resembles a dot product. Indeed, \[ \frac{dz}{dt} = \begin{bmatrix} \frac{\partial z}{\partial x_1} \\ \vdots \\ \frac{\partial z}{\partial x_n} \end{bmatrix} \;\cdot\; \begin{bmatrix} \frac{dx_1}{dt} \\ \vdots \\ \frac{dx_n}{dt} \end{bmatrix} \]
The "factor" on the right is clearly the derivative of the vector valued function $\mathbf{x}(t)$. The "factor" on the left is called the "gradient vector". More on that later.
Directional derivatives of functions in two variables
Recall that partial derivatives of a function $z = f(x,y)$ are essentially the derivatives of $f$ in $x$ and $y$ directions only.
Can we construct a similar "derivative" in any direction?
The answer is Yes, and the result is called "directional derivative".
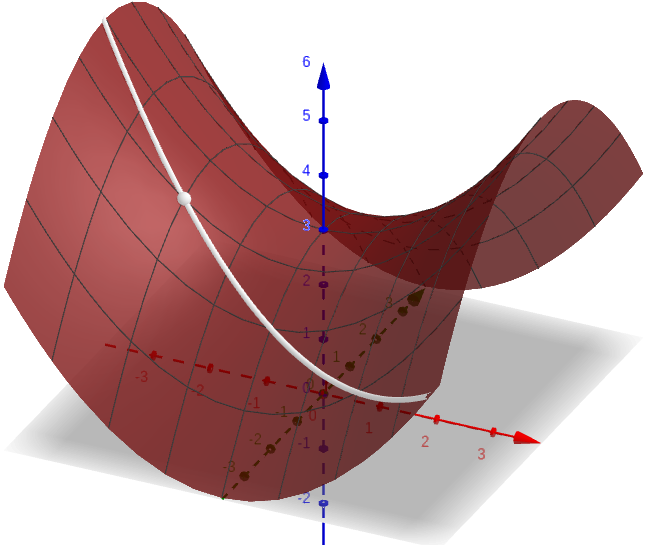
A simpler formulation for directional derivatives
The definition is somewhat difficult to use. Using chain rule, we can derive a more friendly formulation.
As long as the points at which those functions are evaluated are understood, we can write this in a more compact form as \[ D_{\mathbf{v}} f = v_1 \, \frac{\partial f}{\partial x} + v_2 \, \frac{\partial f}{\partial y}. \]
It is also a dot product: \[ D_{\mathbf{v}} f = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix} \cdot \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \]
These results tell us that all directional derivatives of a differentiable function can be computed easily once the partial derivatives are computed.
Exercises
For all the functions listed below, compute the directional derivative $D_{\mathbf{v}}(x,y)$. for any unit vector $\mathbf{v} = (v_1,v_2)$, Can you describe for what choice of $\mathbf{v}$ will directional derivative reaches its maximum? What about minimum?
More general directional derivatives
The geometric interpretation of taking a cross section remains correct here, though we may not be able to visualize it in the familiar 3-dimensional space.
Higher order of directional derivatives can be defined, but we don't have a very good notation for them. (We do have several bad ones)
A warning on non-differentiable functions
The requirement that $f(x,y)$ (or $f(x_1,\ldots,x_n)$ in general) being differentiable is very important. Here we will show what could go wrong if this condition is dropped.
"Counterexamples" like these highlight the importance of the concept of differentiability. In both cases, the functions in question are not differentiable at the origin, hence the problem.