Curvature and torsion

Characterizing the shape of smooth curves

Curvature an torsion are two numbers that can characterize how a smooth curve is turning at a given point.

Parametric space curve

As before, throughout this discussion, we will use the notation \[ \mathbf{r}(t) = \begin{bmatrix} x(t) \\ y(t) \\ z(t) \end{bmatrix} \] to represent a vector-value function. For simplicity, we assume it is defined and differentiable for all $t$ (over the entire real line).

To appeal to our intuition, it may be useful to consider $t$ as time and imagine the function $\mathbf{r}(t)$ describe the trajectory of an object moving in space.

Review of the TNB frame

Recall that, for any given $t$ value such that $\| \mathbf{r}'(t) \| \ne 0$, (principal) unit tangent vector is \[ \mathbf{T}(t) = \frac{\mathbf{r}'(t)}{ \| \mathbf{r}'(t) \| }. \]

If $\mathbf{T}'(t)$ is defined and nonzero at a given $t$-value, the principal unit normal vector at $t$ is \[ \mathbf{N}(t) = \frac{ \mathbf{T}'(t) }{ \| \mathbf{T}'(t) \|}. \]

Furthermore, if $\mathbf{T}(t), \mathbf{N}(t)$ are defined, the binormal vector at $t$ is \[ \mathbf{B}(t) = \mathbf{T}(t) \times \mathbf{N}(t). \]

These three vector are orthogonal to one another, and they form a natural frame of reference of the 3-dimensional space at a given $t$ value. This is the Frenet frame of reference (or simply the TNB frame).

Curvature

The concept of "curvature" provides a numerical quantity that can measure how sharply a smooth curve turns.

It agrees with our intuition: a straight line has 0 curvature, and a circle has a constant curvature, which depends on the radius.

(Alternative) at a $t$ value where $\mathbf{T}'(t)$ and $\mathbf{r}'(t)$ are both defined and $\| \mathbf{r}'(t) \| \ne 0$, the curvature of the curve represented by $\mathbf{r}(t)$ is given by \[ \kappa = \frac{\| \mathbf{T}'(t) \|}{ \| \mathbf{r}'(t) \|}. \]

This is really an "alternative" working definition, and it has the problem that it is undefined whenever $\mathbf{r}'(t) = \mathbf{0}$. We will see a more elegant (but less useful) definition of $\kappa$ in term of arc-length parametrization.

Alternative curvature formula as a cross product

Using the properties of the unit tangent vector, we can see that the curvature can also be computed as \[ \kappa = \frac{ \| \mathbf{r}'(t) \times \mathbf{r}''(t) \| }{ \| \mathbf{r}'(t) \|^3 }, \] which is usually much easier to compute.

Compute the curvature of the curve represented by $\mathbf{r}(t) = a \cos(t) \mathbf{i} + a \sin(t) \mathbf{j} + 0 \mathbf{k}$, for $a > 0$, at any given $t$ value.

Solution. We can compute that \begin{align*} \mathbf{r}'(t) &= -a\sin(t) \mathbf{i} + a\cos(t) \mathbf{j}, & \mathbf{r}''(t) &= - a \cos(t) \mathbf{i} - a \sin(t) \mathbf{j}. \end{align*} Therefore, $\| \mathbf{r}'(t) \| = a$. Moreover, \[ \mathbf{r}'(t) \times \mathbf{r}''(t) = a^2(\sin^2(t) + \cos^2(t)) \mathbf{k} = a^2 \, \mathbf{k}, \] and hence $\| \mathbf{r}'(t) \times \mathbf{r}''(t) \| = a^2$. So $\kappa = a^2 / a^3 = 1/a$, which agrees with our intuition (smaller the circle, higher the curvature).

Curvature of circles and straight lines

Of course, what we just computed generalizes to any circles. In general, a circle of radius $a$ has a constant curvature of $\frac{1}{a}$. This agrees with our intuition that a smaller circle has large curvature, while a large circle has small curvature.

From our working definition, $\kappa = \frac{ \| \mathbf{T}'(t) \| }{ \| \mathbf{r}'(t) \| }$, we can also easily verify that all straight lines have zero curvature, as expected.

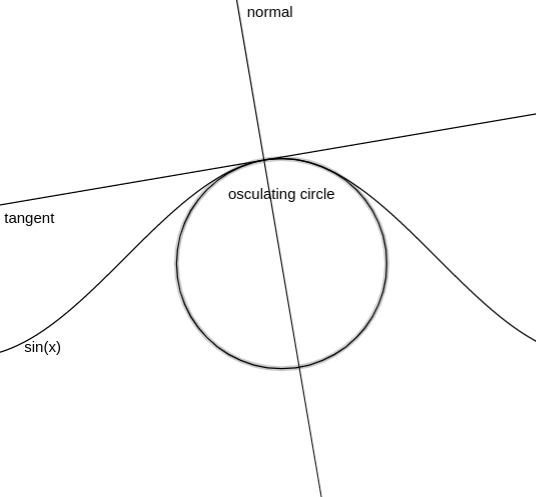
Osculating circle

At any given $t$ value, where $\mathbf{T}(t)$ and $\mathbf{N}(t)$ are both defined, the plane spanned by these two vectors is known as the osculating plane of the curve traced out by $\mathbf{r}(t)$.

In this plane, a circle that is tangent to the curve at $\mathbf{p} = \mathbf{r}(t)$ and has the same curvature is called an osculating circle of the curve at $\mathbf{p}$.

Just like the tangent line is the best linear approximation of a curve at a point, the osculating circle is the best circular approximation of a curve at a point.

Decomposition of acceleration vector

Recall that, if we consider $\mathbf{r}(t)$ to represent the trajectory of a moving object, then its acceleration at any point of time can be decomposed into the tangential component and the normal component. Curvature helps us to describe the normal component.

The acceleration vector $\mathbf{r}''(t)$ of the object, whose trajectory is represented by $\mathbf{r}(t)$, at a given time $t$ lies in the plane spanned by the unit tangent vector $\mathbf{T}(t)$ and the principal unit normal vector $\mathbf{N}(t)$. Moreover, \[ \mathbf{r}''(t) = v'(t) \mathbf{T} + (v(t))^2 \, \kappa(t) \, \mathbf{N}(t), \] where $v(t) = \| \mathbf{r}'(t) \|$ is the speed of the object and $\kappa(t)$ is the curvature of the curve traced out by this object at that moment.

(Here, we have a slight abuse of notation: We express the curvature $\kappa(t)$ as a function of time $t$ since we want to describe how an object moves. But you should keep in mind that $\kappa$ is actually a property of the curve itself.)

Rotation of the osculating plane

By considering $\mathbf{T}'(t)$, we developed the concept of curvature. Now we will consider $\mathbf{B}'(t)$, which characterizes the rotation of the osculating plane itself, and we will develop the concept of torsion from this.

Since $\mathbf{B}(t) = \mathbf{T}(t) \times \mathbf{N}(t)$, by the product rule, \[ \mathbf{B}' = \mathbf{T}' \times \mathbf{N} + \mathbf{T} \times \mathbf{N}' = \mathbf{T}' \times \frac{\mathbf{T}'}{ \| \mathbf{T}' \| } + \mathbf{T} \times \mathbf{N}' = \mathbf{T} \times \mathbf{N}'. \] Therefore, $\mathbf{B}'(t)$ must be orthogonal to $\mathbf{T}(t)$. (That's how cross product works)

Also recall that $\mathbf{B}(t)$ is always a unit vector, so its derivative $\mathbf{B}'(t)$ must be orthogonal to $\mathbf{B}(t)$ itself.

That is, $\mathbf{B}'(t)$ is orthogonal to both $\mathbf{T}(t)$ and $\mathbf{B}(t)$.

Therefore, $\mathbf{B}'(t)$ must be parallel to $\mathbf{N}(t)$. That is, $\mathbf{B}'(t)$ must be a multiple of $\mathbf{N}(t)$, and the coefficient describe how fast and in which direction is the osculating plane rotating about the $\mathbf{N}(t)$.

Torsion

So far, through some vector algebra, we understood that $\mathbf{B}'(t)$ must be a multiple of $\mathbf{N}(t)$. We can visualize this coefficient as a description of how fast and in which direction is the osculating plane rotating about the $\mathbf{N}(t)$. This leads to the concept of torsion.

If $\| \mathbf{r}'(t) \| = 1$, then we define the torsion of the curve represented by $\mathbf{r}$ at a given point to be \[ \tau = - \mathbf{B}'(t) \cdot \mathbf{N}(t). \]

In the more general case where $\| \mathbf{r}'(t) \|$ may not be 1, we have the alternative formula \[ \tau = \frac{ \det [ \mathbf{r}', \mathbf{r}'', \mathbf{r}''' ] }{ \| \mathbf{r}' \times \mathbf{r}'' \|^2 } \]

Comparing the two formula, we can see that the condition $\| \mathbf{r}'(t) \| = 1$ produces much more elegant formula. This is the benefit of "arc-length parametrization", which we will develop in more rigorous context.