Taylor and Maclaurin series

The discussion in the previous lecture shows that within its interval of convergence, a power series represents a function (a very nice function as far as doing calculus is concerned). It is then reasonable to ask: Given a function, can we find a power series that represents the function? This is the main question we want to answer in this lecture.

Another closely related question is: What's the best way to approximate a function with a polynomial?

The motivating question

Can we approximate $y=e^x$ with a polynomial near $x=0$?

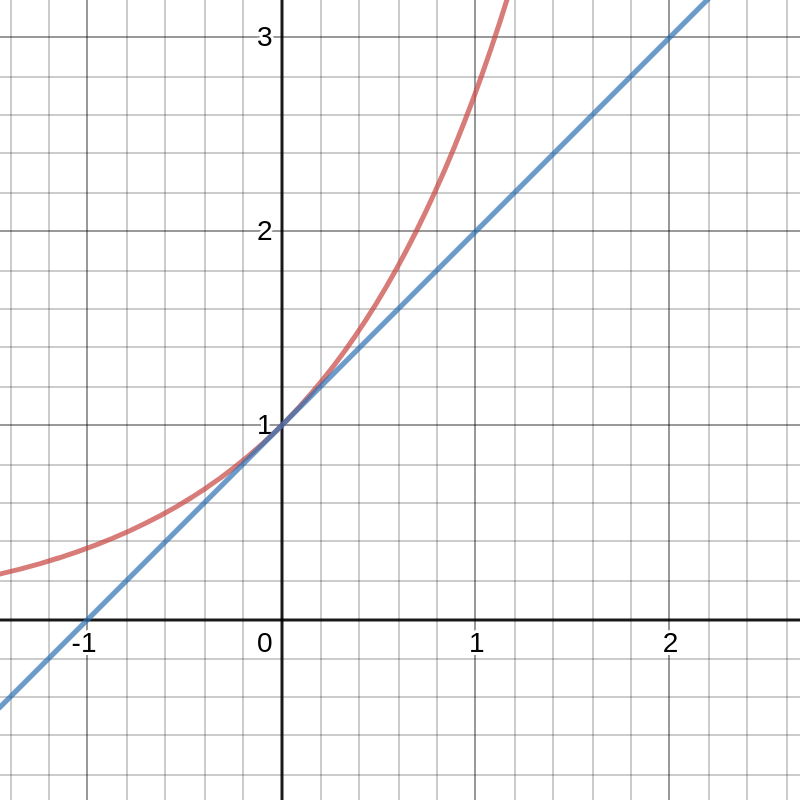
Best linear (1st degree) approximation of $y=e^x$ near $x=0$ is \[ y = 1 + x \] It has the same function value and derivative at $x=0$ as $y=e^x$.

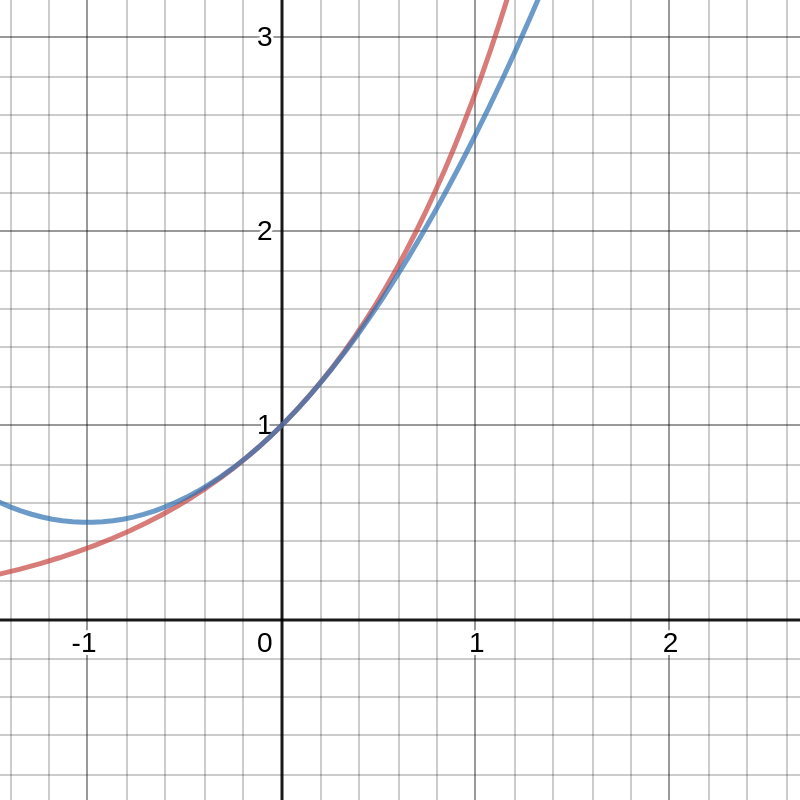
Best quadratic (2nd degree) approximation \[ y = 1 + x + \frac{x^2}{2} \] It has the same function value, same derivative, and same second derivative at $x=0$ as the original function $y=e^x$

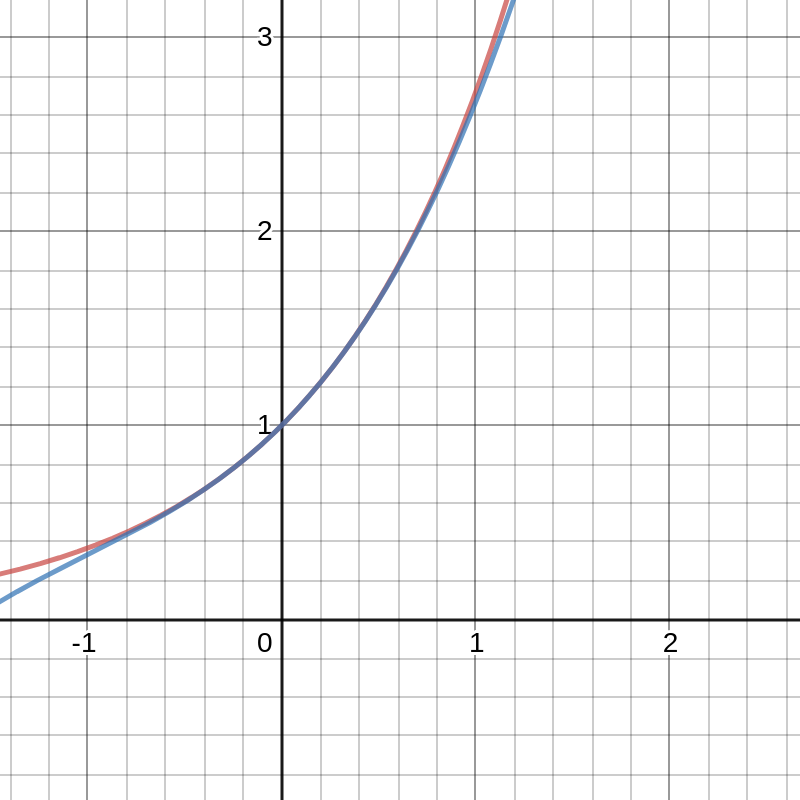
Best cubic (3rd degree) approximation \[ y = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} \] It has the same function value, same derivative, and same second derivative at $x=0$ as the original function $y=e^x$.

We can continue this pattern and reach the formula \[ e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \cdots + \frac{x^k}{k!} + \cdots \]

Taylor and Maclaurin series

The special case of Taylor series of a function $f$ centered at $x=0$ is called the Maclaurin series of $f$.

Recall that the notation $f^{(k)}$ denotes the $k$-th derivative of the function $f$.

Example

Let's apply the formula of Taylor series \[ f(a) + f'(a) (x-a) + \frac{f'' (a)}{2} (x-a)^2 + \frac{f'''(a)}{6} (x-a)^3 + \cdots \] to the function $f(x) = e^x$, centered at $x=0$.

To do that, we need to compute all derivatives of $f(x) = e^x$. Fortunately, this is easy to do for this particular function since \[ f^{(k)} (x) = \frac{d^k}{dx^k} (e^x) = e^x \quad \text{and} \quad e^0 = 1, \]

which means $f^{(k)}(0) = 1$ for any $k$ in this case. Therefore \[ e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \cdots + \frac{x^k}{k!} + \cdots \]

Another example

Let's apply the formula $ f(a) + f'(a) (x-a) + \frac{f'' (a)}{2} (x-a)^2 + \cdots$ to the function $f(x) = \frac{1}{x}$, centered at $x=1$.

Again, to do this, we will need to compute all the derivatives of the function $f(x) = \frac{1}{x} = x^{-1}$ via repeated applications of the "power rule".

What's the point?

The importance of Taylor series lies in its unique ability to represent a function using information from a single point.

The "if" part of the above theorem may not always hold. There are functions that does not agree with any power series on an open interval.

Exercise. Compute the Taylor series of the following functions of $x$ centered at $x=0$, and see if the function agrees with the series. \begin{align*} & e^x & & \sin(x) & & \cos(x) & & \sinh(x) & & \ln(1+x) & & \frac{1}{1-x} \end{align*}

Taylor Polynomials

In many applications, a full Taylor series is often not necessary, and a partial sum may be sufficient. Such a partial sum is called a Taylor polynomial.

For examples, for a function $f(x)$, \begin{align*} p_0(x) &= f(a) \\ p_1(x) &= f(a) + f'(a)(x-a) \\ p_2(x) &= f(a) + f'(a)(x-a) + \frac{f''(a)}{2} (x-a)^2 \\ p_3(x) &= f(a) + f'(a)(x-a) + \frac{f''(a)}{2} (x-a)^2 + \frac{f'''(a)}{6} (x-a)^3 \end{align*} are Taylor polynomials for $f$ at $a$ of degree 0, 1, 2, and 3 respectively.

Taylor polynomial of a function centered at 0 is a Maclaurin polynomial.

Revisiting $e^x$

As we saw earlier, we can approximate the function $f(x) = e^x$ using polynomials near $x=0$. Those are indeed Taylor polynomials.

Degree 1 Taylor polynomial $p(x) = 1 + x$:

Degree 2 Taylor polynomial $p(x) = 1 + x + \frac{x^2}{2}$:

Degree 3 Taylor polynomial $p(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6}$:

Taylor Remainder Theorem

Taylor polynomials are finite approximations of Taylor series. Whether or not this approximation is good depends on the function itself, and the following theorem quantifies how good this approximation can be.

Here $R_n(x) = f(x) - p_n(x)$ is called the $n$-th remainder. The above theorem states that if we can control the magitude of the $n+1$ order derivative of $f$, we can control the remainder $R_n$.