Hyperbolic functions

Coordinate functions for the hyperbola

Hyperbolic sine and hyperbolic cosine are the coordinate functions for the standard equilateral hyperbola, and they are the hyperbolic analog of the sine and cosine.

Hyperbolic functions

Hyperbolic functions are mirror images of the ordinary trigonometric functions constructed using hyperbola (instead of the unit circle). In particular, the "hyperbolic sine" and "hyperbolic cosine" are the coordinate functions for the standard equilateral hyperbola.

They appear naturally in the context of hyperbolic geometry, linear differential equations, classical mechanics, and special relativity (among many other topics). So they are important tools to understand.

Just like sine and cosine for the unit circle

The unit circle is a circle of radius 1 centered at the origin. It can be expressed as the set of all points $(x,y)$ on the plane that satisfy \[ x^2 + y^2 = 1. \]

Ordinary sine and cosine can be understood as coordinate functions for the unit circle: Every point on a unit circle can be expressed as $(x,y)$ with $x = \cos(t)$ and $y = \sin(t)$.

If we replace the unit circle by the equilateral hyperbola, the corresponding coordinate functions we get are the "hyperbolic cosine" and "hyperbolic sine".

A hyperbola is a set of points whose absolute difference of the distances to two fixed points is a constant. The name came from a Greek word that means "excessive" from which we also get the English word hyperbole. In classical Greek mathematics, it is the name of one of the conic sections (the other two are the ellipse and the parabola).

An equilateral hyperbola is a special hyperbola consisting of points $(x,y)$ satisfying the equation \[ x^2 - y^2 = 1. \]

Note the similarity to the definition of the unit circle. If we express the coordinates $x$ and $y$ as two functions of a variable $t$, we end up with hyperbolic sine and cosine functions.

Without calculators/computers, can you visualize what this curve look like?

Given any real number $t$, the value of the hyperbolic sine and hyperbolic cosine are given by \begin{align*} \sinh(t) &= \frac{e^t - e^{-t}}{2} \\ \cosh(t) &= \frac{e^t + e^{-t}}{2} \end{align*} respectively.

From what we know about the exponential function, it is easy to verify that these two functions are

defined,
continuous,
differentiable, and
Riemann integrable

over any interval.

Equilateral hyperbola

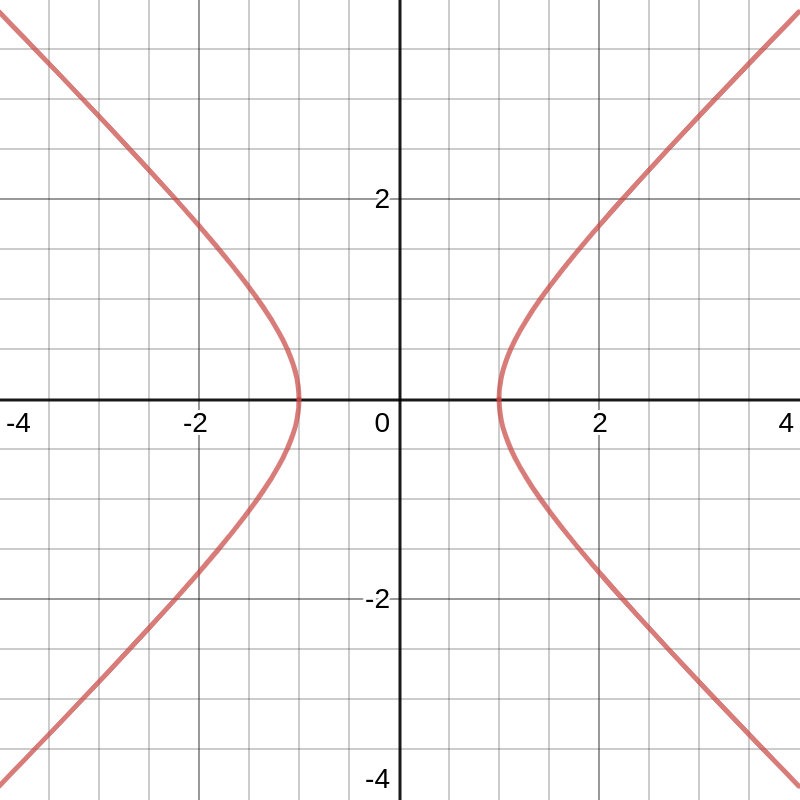
This is the standard equilateral hyperbola defined by the equation \[ x^2 - y^2 = 1. \] It is one of the conic sections, and it naturally appear in many applications.

In the following discussion, we only focus on the "right half" of this object, which is the subset of the points with positive $x$-coordinates.

Hyperbola are of special importance in special relativity: the trajectory of an object with constant proper acceleration can be visualized as a hyperbola on a Minkowki diagram.

The two functions, \begin{align*} \sinh(t) &= \frac{e^t - e^{-t}}{2} \\ \cosh(t) &= \frac{e^t + e^{-t}}{2} \end{align*} are the coordinate functions of the equilateral hyperbola.

For any real number $t$, letting $x = \cosh(t)$ and $y = \sinh(t)$ will produce a point $(x,y)$ on the right half of the equilateral hyperbola.

Conversely, for any point $(x,y)$ on the right half of the equilateral hyperbola, we can find a $t$ such that $x = \cosh(x)$ and $y = \sinh(y)$.

Verify that $x = \cosh(t)$ and $y = \sinh(t)$ satisfy \[x^2 - y^2 = 1.\]

Without using calculator/computer, can you visualize what the graphs of these two functions look like?

Properties

The two functions $\cosh(t)$ and $\sinh(t)$ also appear naturally in other context. For instance, we can verify that \[ \cosh(t) + \sinh(t) = e^{t}. \] Indeed $\cosh(t)$ and $\sinh(t)$ are exactly the even part and the odd part of the exponential function $e^t$.

Both $\cosh$ and $\sinh$ are differentiable everywhere.

$\frac{d}{dt} \cosh(t) = \sinh(t)$
$\frac{d}{dt} \sinh(t) = \cosh(t)$
$\int \sinh(t) dt = \cosh(t)$
$\int \cosh(t) dt = \sinh(t)$.

Verify that $\cosh(t)$ is an even function and $\sinh(t)$ is an odd function.

Derive formula for $\sinh(a+b)$ and $\cosh(a+b)$ (similar to the sum-to-product formula for sine and cosine)?

Connections to differential equations

From this we can see $\cosh$ and $\sinh$ are solutions to the equation \[ y'' = y, \] which is an equation that show up naturally in physics and engineering.

Side note: Indeed, $\cosh$ and $\sinh$ are "linear independent" and they form a "fundamental set" of solutions to the differential equation $y''=y$. Moreover, they satisfies the initial conditions \[ y(0) = 1 \quad y'(0) = 0 \] and \[ y(0) = 0 \quad y'(0) = 1 \] respectively. These properties make the especially desirable type of solutions in physics and engineering.

Other hyperbolic functions

Just like how you can define other trigonometric functions in terms of sine and cosine, we can define additional hyperbolic functions in terms of hyperbolic sine and cosine.

We define the hyperbolic tangent to be \[ \tanh(x) = \frac{\sinh(x)}{\cosh(x)}. \]

We define the hyperbolic cotangent to be \[ \coth(x) = \frac{\cosh(x)}{\sinh(x)} \]

Following from the quotient rule, we can see that \begin{align*} \frac{d}{dx} \tanh(x) &= 1 - \tanh^2(x), \\ \frac{d}{dx} \coth(x) &= 1 - \coth^2(x). \end{align*}

It is worth noting that $\coth(x)$ is undefined at $x=0$, where it has an vertical asymptote.