What is sound?

In physics, sound is simply vibration propagates as an acoustic wave in some medium.

For most of us, this is simply the vibration of air. And in air, sound is transmitted as "longitudinal waves", a.k.a. "compression waves". (Change in air pressure over time)

Creating sound out of sine and cosine

We can generate a pressure wave, in air, with relative pressure given by \[ f(t) = A \sin (k \cdot 2\pi t) \] where $A$ and $k$ are positive real numbers representing amplitude and frequency of the wave. This models actual waves very accurately.

It is convenient to use second as the unit for $t$ (time). While the standard unit for $A$ (and hence $f$ itself) should be Pascal, this is rarely used. Instead, $A$ is usually expressed as percentage (e.g. 25%, 90%, etc). The standard unit for $k$ is hertz (Hz).

Amplitude and frequency

In the wave, \[ f(t) = A \sin (k \cdot 2\pi t) \] the amplitude roughly correspond to loudness (although loudness is a complicated function of amplitude).

The frequency, $k$ (measured in Hz), corresponds to pitch (i.e., higher or lower notes).

Our ears can hear certain range of amplitude and frequency. Do you know the human hearing range? What about that for dogs?

Scalar multiple of a sine wave

For a wave, \[ f_0(t) = \sin (440 \cdot 2 \pi t) \] scalar multiple of $f_0$ with a positive $r \in \mathbb{R}$, \[ r \cdot f_0(t) = r \sin (440 \cdot 2 \pi t) \] corresponds to a change of amplitude (louder or quieter).

Negative scalars can also be used, but they will also invert the "phase".

Sum of sine waves

Two sine waves of different frequencies can be added together (as functions), e.g. \[ \sin (440 \cdot 2 \pi t) + \sin (880 \cdot 2 \pi t) \]

This operation corresponds to playing/hearing two sound at the same time. (That's how waves combine)

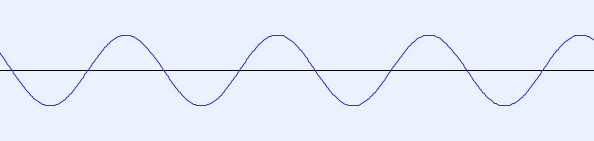
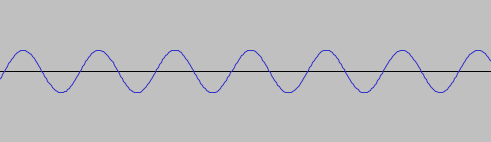
Linear combinations

By combine scalar multiplication and sum of sine waves, we can create linear combinations of waves, e.g. \[ a \cdot f_1(t) + b \cdot f_2(t). \] Can you interpret the physical meaning of this operation?

In general, it is possible to combine an arbitrary number of sine waves through linear combinations: \[ \sum_{k=1}^n a_k \cdot f_k(t) \] where each $f_k$ is a sine wave and $a_k$ is a real number.

Infinite sum

In general, we can consider arbitrary linear combinations of sine waves of frequencies 1Hz, 2Hz, 3Hz,... (to infinity)

\[ \sum_{k=1}^\infty a_k \sin(k \cdot 2\pi t) \]

In more rigorous studies, we must consider the question of convergence. In this course, for simplicity, we will ignore this question and only consider the symbolic aspect of such sums.

Phase

So far we only considered the frequencies of sine waves.

There is another parameter: phase, which allows us to shift the graph of sine horizontally and construct general "sine-like" waves.

• $A$ is still the amplitude (peak deviation from zero).
• $k$ still is the frequency (number of cycles over $[0,1]$).
• $\phi$ is the phase (horizontal shift of the graph).

What we discussed previously is simply the special case of $\phi = 0$.

Cosine waves are sine waves too

Recall that \[ \cos(t) = \sin(t + \pi/2). \] That is, cosine is exactly a shifted version of the sine function. (We shift the graph of sine to the left by $\pi/2$)

Therefore, cosine waves are sine waves (sinusoids) too!

Sine-cosine form

The expression \[ A \sin(2k\pi t + \phi), \] for a general sine wave is not very convenient for computation. An equivalent sine-cosine form is generally preferred.

Using trig. identities, the above can be transformed into \[ a \cos(2k\pi t) + b \sin(2k\pi t), \] where $a,b$ are real numbers that can be computed from $A$ and $\phi$.

In this form, the amplitude and phase are "hiding" inside in $a$ and $b$.

Linear combinations of sine waves

Like before, we can consider linear combinations of sine waves, e.g., \[ \alpha A_1 \sin(2k_1\pi t + \phi_1) + \beta A_2 \sin(2k_2\pi t + \phi_2). \]

...or in the sine-cosine form \[ \alpha [a_1 \cos(2k_1 \pi t) + b_1 \sin(2k_1 \pi t)] + \beta [a_2 \cos(2k_2 \pi t) + b_2 \sin(2k_2 \pi t)]. \]

Linear combinations of sine waves of different frequencies may not be sine waves. (But we will still call them waves)

This is a good thing! By combining different sine waves, we can create much more interesting functions. And that's the whole point!

Vector space of waves

For range of frequencies, say $k=1,\ldots,N$, we consider the set \[ V = \left\{ \sum_{k=1}^N a_k \cos(2k\pi t) + b_k \sin(2k\pi t) \;:\; a_k,b_k \in \mathbb{R} \right\}. \] which include combinations of sine waves of 1 Hz, 2 Hz, ..., $N$ Hz (as well as all different phase parameters).

$V$ has a natural vector space structure derived from the linear combination of waves.

I.e., it is closed under linear combinations. The zero element, as expected, is the zero function $f(t) = 0$ (a sine wave of zero amplitude).

$V$ is fundamentally different from $\mathbb{R}^n$, yet it also forms a vector space. As such, combinations of sine waves can be legitimately called vectors.

Interpretations

The vector space \[ V = \left\{ \sum_{k=1}^N a_k \cos(2k\pi t) + b_k \sin(2k\pi t) \;:\; a_k,b_k \in \mathbb{R} \right\}, \] equipped with scalar multiplication and addition, include combinations of sine waves of 1 Hz, 2 Hz, ..., $N$ Hz with all different phase values.

Length, angle, and inner product?

In the vector space \[ V = \left\{ \sum_{k=1}^N a_k \cos(2k\pi t) + b_k \sin(2k\pi t) \;:\; a_k,b_k \in \mathbb{R} \right\}, \] elements ("vectors") are combinations of sine waves.

Does it makes sense to talk about the length of these waves? What about angles between waves?

Recall that in $\mathbb{R}^n$, such concepts came from inner/dot products. So the key question is: "Do we have inner product between waves?"

Inner product

Now, we will define inner product for waves in \[ V = \left\{ \sum_{k=1}^N a_k \cos(2k\pi t) + b_k \sin(2k\pi t) \;:\; a_k,b_k \in \mathbb{R} \right\}. \]

For this to make sense, we need $f$ and $g$ to be "square integrable", which is satisfied by construction. But this topic is outside the scope of our discussion.

The interval $\left[ -\frac{1}{2},\frac{1}{2} \right]$ is arbitrary: Any interval covering one period of $f(t) = \sin(2\pi t)$ may be used. This one makes computation easier.

Norm of waves (strange as it may seem)

This is a generalization of "length", and it is now very much detached from our geometric intuition. (Visualization is unlikely to be helpful)

Unit vector/waves

Naturally, we say a vector (wave) $f$ is a unit vector if $\|f\| = 1$, i.e., \[ \int_{-\frac{1}{2}}^{\frac{1}{2}} [f(t)]^2 \, dt = 1. \]

Angle between "unit" waves

For $f,g$ in this space such that $\|f\| = \| g \| = 1$, we can show that $\langle f, g \rangle$ must be between $-1$ and $1$. (a consequence of the Cauchy-Schwarz inequality).

This happens to be the range of the cosine function.

So it is meaningful to define the angle $\theta$ between $f$ and $g$ to be the real number (in $[0,\pi)$) such that \[ \cos \theta = \langle f, g \rangle. \]

Angle between waves, in general

For nonzero waves $f$ and $g$, we define the angle between them to be \[ \theta = \cos^{-1} \left( \frac{ \langle f, g \rangle }{ \| f \| \| g \| } \right). \]

It may feel rather strange to talk about angle between waves, but this is a generalization of angle between geometric vectors.

Strange or not, it is actually quite useful, as it allows us to talk about orthogonality in this space.

Orthogonal waves

Following our definition of "angles" between waves, we say two waves $f$ and $g$ are orthogonal to each other if \[ \langle f, g \rangle = 0. \]

That is, \[ 0 = \langle f, g \rangle = \int_{-\frac{1}{2}}^{\frac{1}{2}} f(t) \, g(t) \, dt. \]