Linear least squares problems
Finding best solutions to $Ax \approx b$
The linear least squares problem is one of the fundamental problems in numerical computations and it is closely linked to many problems in data science.
Review: linear systems
Recall that a system of linear equations can be expressed as \[ A \mathbf{x} = \mathbf{b} \] where $A$ contains the coefficients, $\mathbf{x}$ is a column vector containing the unknowns, and $\mathbf{b}$ collects the constant terms on the r.h.s.
Such a linear system has natural geometric interpretations.
There are multiple different geometric interpretations, depending on our point of views.
Holding these very different interpretations at the same time is an important skill we need to develop.
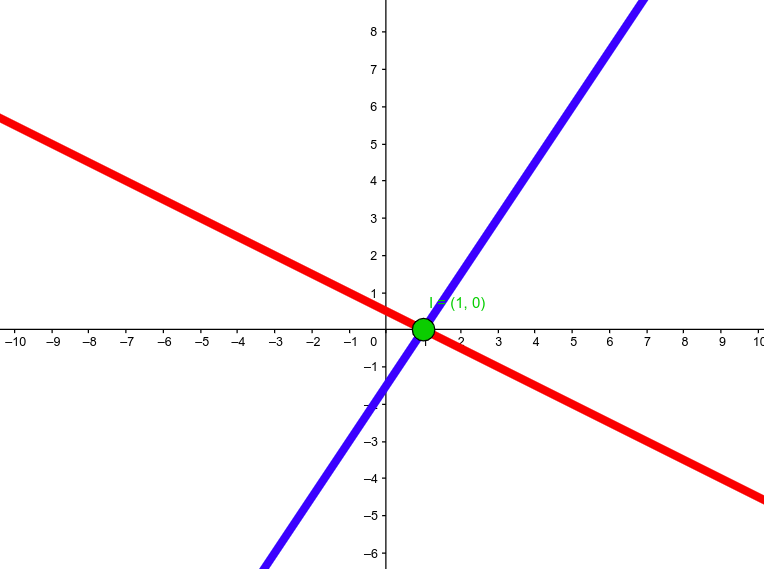
"Row" interpretation: intersecting lines
\[ \left\{ \begin{aligned} 1x + 2y &= 1 \\ 3x - 2y &= 3 \end{aligned} \right. \]
is equivalent to the problem of intersecting two lines.
Column interpretation
The system of equations \[ \left\{ \begin{aligned} 1x + 2y &= 1 \\ 3x - 2y &= 3 \end{aligned} \right. \] is equivalent to \[ x \, \begin{bmatrix} 1 \\ 3 \end{bmatrix} + y \, \begin{bmatrix} 2 \\ -2 \end{bmatrix} = \begin{bmatrix} 1 \\ 3 \end{bmatrix} \]
Overdetermined system
Using the "row" interpretation, it is easy to see why a system of 3 equations in 2 unknowns may not have a solution (unless the configuration of the 3 lines is very "special").
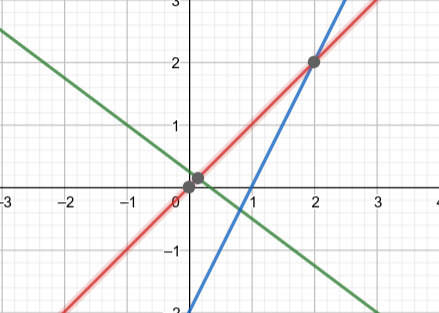
When there is no solution......
It is common, in applications, to encounter linear systems that has no solutions, i.e., we cannot there is no $\mathbf{x}$ such that \[ A \mathbf{x} = \mathbf{b}. \]
The next best thing is to find the "best" solution to \[ A \mathbf{x} \approx \mathbf{b} \]
But what does "best" mean?
One choices is to minimize the difference between $A \mathbf{x}$ and $\mathbf{b}$, which is known as the residual.
That is, we aim to find $\mathbf{x}$ that will minimize $\| A \mathbf{x} - \mathbf{b} \|$. For technical reasons (calculus), it is much easier to minimize the square of this instead.