Root counting, tropical intersection, homotopy, and networks of oscillators
Tianran Chen
Department of Mathematics and Computer Science
Auburn University at Montgomery
April 14, 2019
MAAG 2019 Georgia Tech
Joint work with Robert Davis and Dhagash Mehta
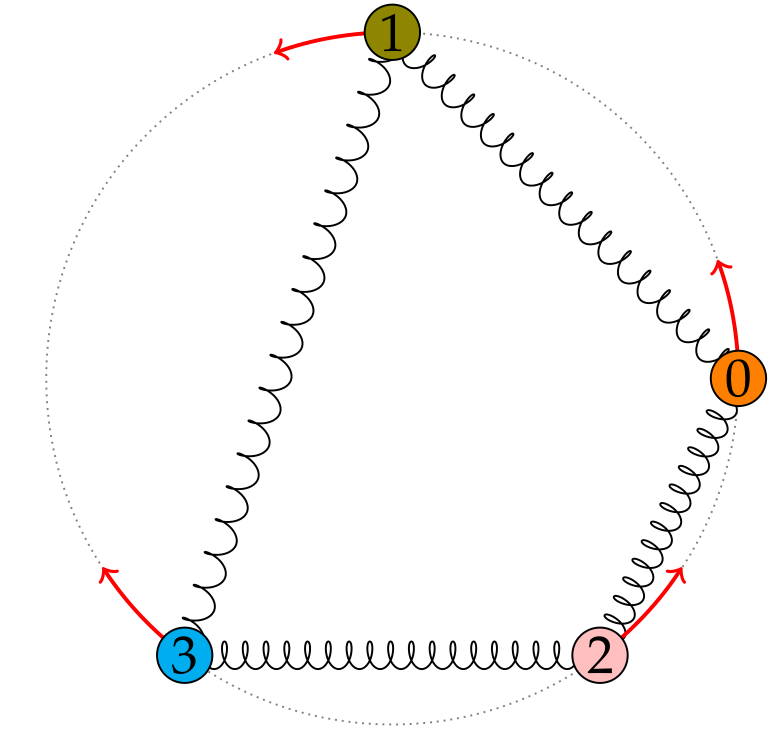
Oscillator: an object varying between two states.
- heart cells
- neurons
- chemical oscillators
- AC generators
- ...
Coupled oscillators
Kuramoto model (Y. Kuramoto 1975)
\[ \dot{\theta}_i = \omega_i - \sum_{j=0}^n k_{ij} \sin(\theta_i - \theta_j) \]
A balance between simple formulation and complex behavior
Frequency synchronization configuration
Configurations of $(\theta_1,\dots,\theta_n)$ for which $\dot{\theta}_i$ are the same:
\[ c = \omega_i - \sum_{j=0}^n k_{ij} \sin(\theta_i - \theta_j) \]
... they are equivalent to critical points defined by \[ 0 = \omega_i - \sum_{j=0}^n k_{ij} \sin(\theta_i - \theta_j) \]
Algebraic geometry approaches to this problem:
-
J. Baillieul and C. Byrnes
Geometric Critical Point Analysis of Lossless Power System Models
-
D. Mehta, N. Daleo, F. Dörfler, and J. Hauenstein
Algebraic geometrization of the Kuramoto model: Equilibria and stability analysis
-
O. Coss, J. Hauenstein, H. Hong, and D. Molzahn
Locating and Counting Equilibria of the Kuramoto Model with Rank-One Coupling
\[ \begin{aligned} \omega_0 &= k_{01} \sin(\theta_0 - \theta_1) + k_{02} \sin(\theta_0 - \theta_2) \\ \omega_1 &= k_{10} \sin(\theta_1 - \theta_0) + k_{13} \sin(\theta_1 - \theta_3) \\ \omega_2 &= k_{20} \sin(\theta_2 - \theta_0) + k_{23} \sin(\theta_2 - \theta_3) \\ \omega_3 &= k_{31} \sin(\theta_3 - \theta_1) + k_{32} \sin(\theta_3 - \theta_2) \end{aligned} \]
Consider complex phase angles
\[ \theta_i \;\mapsto\; z_i = \theta_i - \mathbf{i}\, r_i \]
and the change of variables
\[
x_i = e^{\mathbf{i} z_i} = e^{r_i + \mathbf{i}\,\theta_i}
\]
\[
\sin(z_i - z_j) = \frac{
e^{\mathbf{i}z_i - \mathbf{i}z_j} -
e^{\mathbf{i}z_j - \mathbf{i}z_i}
}{2\mathbf{i}}
=
\frac{1}{2\mathbf{i}} \left(
\frac{x_i}{x_j} - \frac{x_j}{x_i}
\right)
\]
\[
\theta_i
\;\longrightarrow\;
z_i = \theta_i - \mathbf{i}\, r_i
\;\longrightarrow\;
x_i = e^{\mathbf{i} z_i}
\]
The synchronization equations
\[
0 = \omega_i - \sum_{j=0}^n k_{ij} \sin(\theta_i - \theta_j)
\]
becomes the Algebraic Kuramoto Equations
\[
0 = \omega_i - \sum_{j=0}^n a_{ij}'
\left(
\frac{x_i}{x_j} - \frac{x_j}{x_i}
\right)
\]

\[ \begin{aligned} \omega_0 &= a_{01}' (x_0 / x_1 - x_1 / x_0) + a_{02}' (x_0 / x_2 - x_2 / x_0) \\ \omega_1 &= a_{10}' (x_1 / x_0 - x_0 / x_1) + a_{13}' (x_1 / x_3 - x_3 / x_1) \\ \omega_2 &= a_{20}' (x_2 / x_0 - x_0 / x_2) + a_{23}' (x_2 / x_3 - x_3 / x_2) \\ \omega_3 &= a_{31}' (x_3 / x_1 - x_1 / x_3) + a_{32}' (x_3 / x_2 - x_2 / x_3) \end{aligned} \]
Algebraic Kuramoto Equations:
\[
0 = \omega_i - \sum_{j=1}^n a_{ij}'
\left(
\frac{x_i}{x_j} - \frac{x_j}{x_i}
\right)
\]
- How many solutions?
- How to find all solutions?
- What can network topology tell us?
- Can we decompose large networks?
Root counting
\[ \begin{aligned} \omega_1 &= a_{10}' (x_1 / x_0 - x_0 / x_1) + a_{13}' (x_1 / x_3 - x_3 / x_1) \\ \omega_2 &= a_{20}' (x_2 / x_0 - x_0 / x_2) + a_{23}' (x_2 / x_3 - x_3 / x_2) \\ \omega_3 &= a_{31}' (x_3 / x_1 - x_1 / x_3) + a_{32}' (x_3 / x_2 - x_2 / x_3) \end{aligned} \]
- Bezout number
- Bi-homogeneous Bezout number
- BKK bound
- Intersection of tropical hypersurfaces
- Birationally invariant intersection index
BKK bound
Theorem (Bernshtein-Kushnirenko-Khovanskii)
Given a system of Laurent polynomials $f_1,\dots,f_n$ in $(x_1,\dots,x_n)$ with generic coefficients, the number of isolated common roots in $(\mathbb{C}^*)^n$ is bounded by
\[ \text{MVol}(\text{Newt}(f_1),\dots,\text{Newt}(f_n)) \]
\[ \text{Minkowski sum: } A + B := \{ a + b \mid a \in A, b \in B \} \]
Mixed volume (Minkowski)
For convex polytopes $P_1,\dots,P_n$ in $\mathbb{R}^n$, the mixed volume $\text{MVol}(P_1,\dots,P_n)$ is the coefficient of $\lambda_1 \cdots \lambda_n$ in \[ \text{vol}(\lambda_1 P_1 + \cdots + \lambda_n P_n) \]
$\text{MVol}(A,B) = \text{Coef. of } \lambda_1 \lambda2 \text{ in } (\lambda_1 A + \lambda_2 B)$
Root count for the Algebraic Kuramoto equations
\[ 0 = \omega_i - \sum_{j=0}^n a'_{ij} \left( \frac{x_i}{x_j} - \frac{x_j}{x_i} \right) \]
can be computed as the BKK bound ???
Intersection index (Kaveh & Khovanskii)
Given an irreducible $n$-dimensional toric variety $X$ and finite dimensional vector spaces of rational functions $L_1,\dots,L_n$ on $X$, the number of common zeros of $(f_1,\dots,f_n)$ in $X$ for generic choices of $f_1 \in L_1$, $\ldots$, $f_n \in L_n$ is the birationally invariant intersection index
\[ [\;L_1 \,,\, \ldots\,,\, L_n\;] \]
Generalization of the BKK bound
(Mixed volume of Newton-Okounkov bodies)
Is is possible to have
$\text{B.I.I.I.} \equiv \text{BKK bound}$ ?
Theorem (C.)
Suppose each $L_i = \text{span}_{\mathbb{C}}\{P_{ij}\}$ for some Laurent polynomials $P_{ij}$'s. If each $\text{Newt}(L_i)$ is full dimensional and every positive-dimensional proper faces of it intersects $\text{Newt}(P_{ij})$ at no more than one point, then
\[
[ L_1, . . . , L_n ] \;=\;
\text{MVol} ( \text{Newt}(L_1), . . . , \text{Newt}(L_n) ).
\]
Consider the algebraic Kuramoto equations
\[ \begin{aligned} -\omega_1 + a_{10}' (x_1 / x_0 - x_0 / x_1) + a_{12}' (x_1 / x_2 - x_2 / x_1) \\ -\omega_2 + a_{20}' (x_2 / x_0 - x_0 / x_2) + a_{21}' (x_2 / x_1 - x_1 / x_2) \\ \end{aligned} \]
Proposition
Given a complete graph, for generic choices of the coefficients, the complex root count (b.i.i.i.) of algebraic Kuramoto equations \[ 0 = \omega_i - \sum_{j=1}^n a_{ij}' \left( \frac{x_i}{x_j} - \frac{x_j}{x_i} \right) \] is exactly the BKK bound.
| B.i.i.i. | $\to$ | BKK bound | $\to$ | Volume? |
| Mixed volume of N.O. bodies | Mixed volume of Newton polytopes | Volume of a single polytope |
Theorem (C.)
If $A$ and $B$ "touch" all the edges of $\text{conv}(A \cup B)$, then
\[ \text{MVol}(A,B) \;=\; \text{Vol}_2( \text{conv} (A \cup B) ) \]
Mixed volume $\longrightarrow$ normalized volume
For $\varnothing \ne S_1,\dots,S_n \subset \mathbb{Z}^n$, let $\tilde{S} = S_1 \cup \cdots \cup S_n$. If every positive dimensional face $F$ of $\text{conv}(\tilde{S})$ satisfies
- $F \cap S_i \ne \varnothing$ for all $i \in \{1,\dots,n\}$; or
- $F \cap S_i$ is a singleton for some $i \in \{1,\dots,n\}$; or
- For each $i \in I := \{ i \mid F \cap S_i \ne \varnothing \}$, $F \cap S_i$ is contained in a $|I|$-dimensional coordinate subspace in which and its projection of dimension less than $|I|$ then
\[ \text{MVol} (\text{conv}(S_1), \dots, \text{conv}(S_n)) = \text{Vol}_n (\text{conv}(\tilde{S})). \]
Much more general equivalence results exist for
mixed volume and semi-mixed volume.
- C. "Unmixing the mixed volume computation"
- F. Bihan & I. Soprunov "Criteria for Strict Monotonicity of the Mixed Volume of Convex Polytopes"
Definition: Adjacency polytope
For a graph $G$ with nodes $\{0,1,\ldots,n\}$,
\[ \nabla_G \;:=\; \text{conv} \{ \pm(\mathbf{e}_i - \mathbf{e}_j) \mid \{i,j\} \in E(G) \} \] where $\mathbf{e}_0 = \mathbf{0}$.
| $\pm(\mathbf{e}_0 - \mathbf{e}_1)$ |
| $\pm(\mathbf{e}_1 - \mathbf{e}_2)$ |
| $\pm(\mathbf{e}_2 - \mathbf{e}_0)$ |
Convex hull of the union of the Newton polytopes
Theorem (C.)
For a cycle graph $C_N$ of $N$ nodes, the corresponding Kuramoto equations with generic coefficients the total number of complex solutions it has is exactly
\[ \text{Vol}_{N-1}(\nabla_{C_N}) \]
(normalized volume of the adjacency polytope)
Generalizations
- Trees
- Complete graphs
- Cycles glued together along an single edge
|
Adjacency polytopes for complete graphs |
$\longrightarrow$ |
Root system polytopes |
Symmetric edge polytope: Matsui, Higashitani, Nagazawa, Ohsugi, Hibi. 2011
Fundamental polytope: Delucchi & Hoessly 2019
Theorem (C., R. Davis, D. Mehta)
For tree networks of $N$ oscillators, the algebraic Kuramoto system has at most $2^{N-1}$ isolated complex solutions.
For cycle networks of $N$ oscillators, the algebraic Kuramoto system has at most $N\binom{N-1}{\lfloor (N-1)/2 \rfloor}$ isolated complex solutions.
These bound may be attained by just real solutions: (Zachariah, Charles, Boston, Lesieutre 2018)
Adjacency polytope
| Volume | $\longrightarrow$ | Root count |
| Facets | $\longrightarrow$ | Directed subnetworks |
Directed edges
\[
0 = \omega_i - \sum_{j=1}^n a_{ij}'
\left(
\frac{x_i}{x_j} - \frac{x_j}{x_i}
\right)
\]
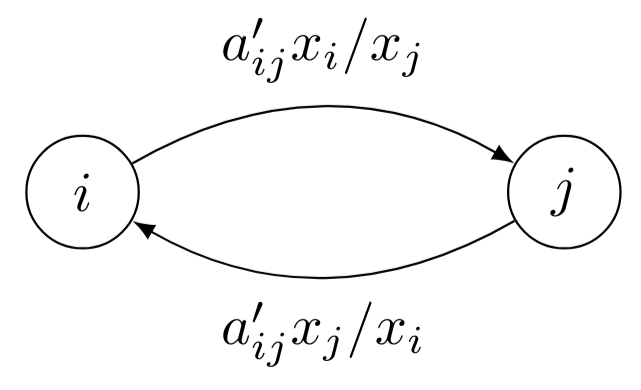
Directed Kuramoto equations
Generalized Kuramoto equations: \[ c_i - \sum_{(i,j) \in \mathcal{E}(G)} a_{ij} \frac{x_i}{x_j} \]
Similar approach: Delabays, Jacquod & Dörfler The Kuramoto model on oriented and signed graphs
Directed acyclic decomposition
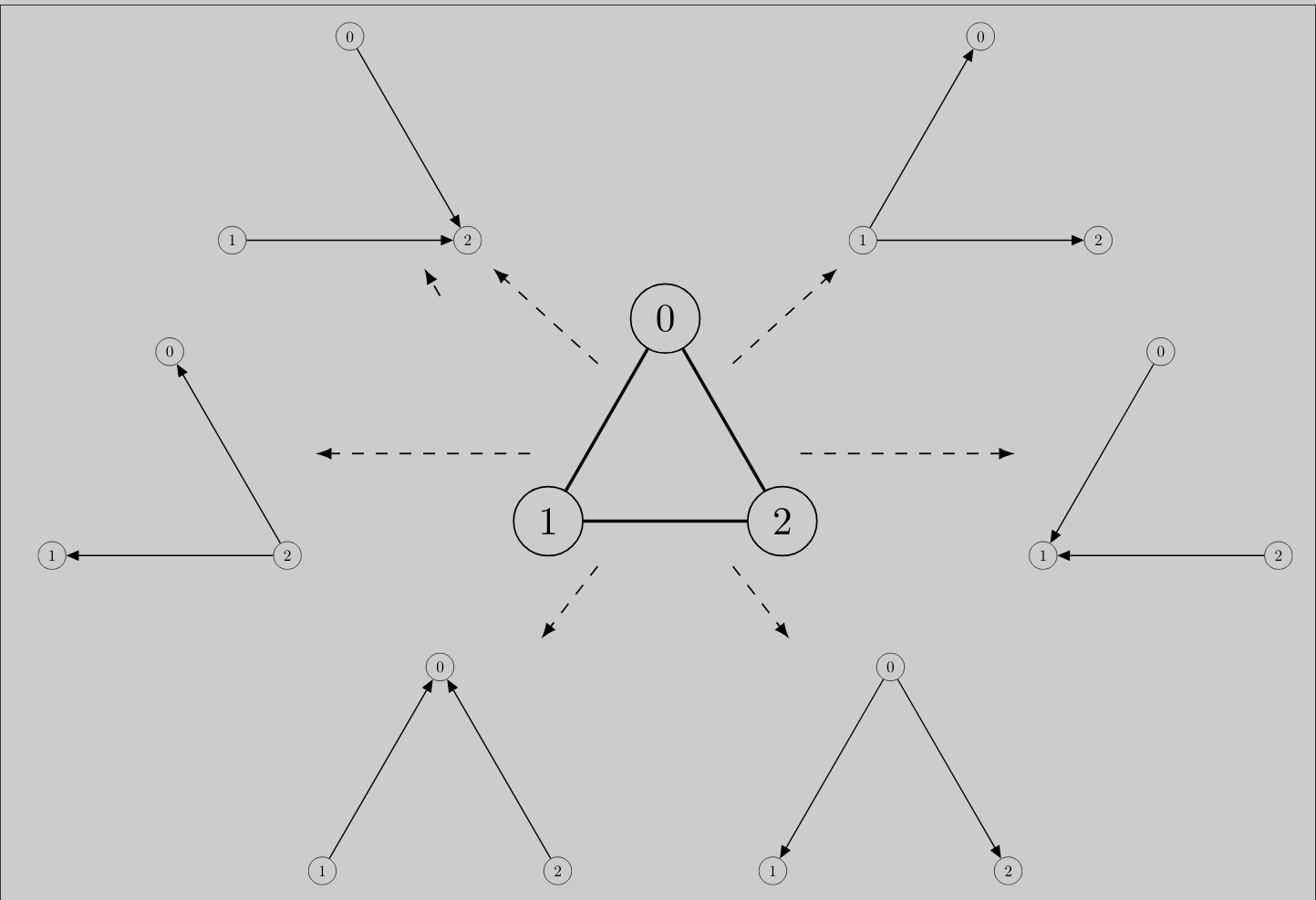
3 oscillators has at most 6 synchronization configurations.
Subnetworks and adjacency polytope
Deformation (adjacency polytope homotopy)
We define $H(x_0,x_1,x_2,t)=(h_0,h_1,h_2)$ given by
\[ \begin{aligned} h_0 &= \frac{\omega_0}{t} - \left[ a_{01}' \left(\frac{x_0}{x_1} - \frac{x_1}{x_0}\right) + a_{02}' \left(\frac{x_0}{x_2} - \frac{x_2}{x_0}\right) \right] \\ h_1 &= \frac{\omega_1}{t} - \left[ a_{10}' \left(\frac{x_1}{x_0} - \frac{x_0}{x_1}\right) + a_{12}' \left(\frac{x_1}{x_2} - \frac{x_2}{x_1}\right) \right] \\ h_2 &= \frac{\omega_2}{t} - \left[ a_{21}' \left(\frac{x_2}{x_1} - \frac{x_1}{x_2}\right) + a_{20}' \left(\frac{x_2}{x_0} - \frac{x_0}{x_2}\right) \right] \end{aligned} \]
which is a continuous deformation of the original system
As $t \to 0$, the solutions escape $(\mathbb{C}^*)^3 = (\mathbb{C} \setminus \{0\})^3$.
...and approach limit set at $t=0$ defined by
\[ \begin{aligned} \omega_1 &= a_{110} x_1 / x_0 + a_{120} x_2 / x_0 \\ \omega_2 &= a_{210} x_1 / x_0 + a_{220} x_2 / x_0 \end{aligned} \]

Deformation to facets
\[ \begin{aligned} h_0 &= \frac{\omega_0}{t} - \left[ a_{01}' \left(\frac{x_0}{x_1} - \frac{x_1}{x_0}\right) + a_{02}' \left(\frac{x_0}{x_2} - \frac{x_2}{x_0}\right) \right] \\ h_1 &= \frac{\omega_1}{t} - \left[ a_{10}' \left(\frac{x_1}{x_0} - \frac{x_0}{x_1}\right) + a_{12}' \left(\frac{x_1}{x_2} - \frac{x_2}{x_1}\right) \right] \\ h_2 &= \frac{\omega_2}{t} - \left[ a_{21}' \left(\frac{x_2}{x_1} - \frac{x_1}{x_2}\right) + a_{20}' \left(\frac{x_2}{x_0} - \frac{x_0}{x_2}\right) \right] \end{aligned} \]
as $t \to 0$ the solution set deform into limit sets at "infinity"
...defined by each facet subsystems
General construction: \[ h_i(\theta_1,\ldots,\theta_{n},t) = \frac{\omega_i}{t} - \sum_{j=0}^n a_{ij}' \left( \frac{x_i}{x_j} - \frac{x_j}{x_i} \right) \]
Advantages over polyhedral homotopy:
- Skips mixed volume computation step
- Structure preserving
- Starting systems have "meanings"
- Involving 0-1 liftings only
A cycle of 5 oscillators has 30 subnetworks.

Proposition (Topology of facet subnetworks)
The underlying directed graph of a facet subnetwork has the following properties:
- it is acyclic;
- it contains all the nodes;
- all paths between a pair of nodes have the same length;
- each paths contains no more than half of the edges of any undirected cycle in the original graph.
Definition (Primitive subnetwork)
A subnetwork is called primitive if the underlying graph is a connected, acyclic, and has $N-1$ directed edges.
Proposition
The facet subsystem corresponding to a primitive subnetwork defines a irreducible toric variety.
Primitive subnetworks give rise to "simple" solution sets
When will a facet subnetwork be primitive?
Theorem
For a tree graph, all facet subnetworks are primitive.
Theorem
For a cycle graph $C_N$, if $N$ is odd then all facet subnetworks are primitive.
Direct acyclic decomposition:
- Deform a Kuramoto equations
- ...onto the facets of its adjacency polytope
- ...leads to facet subsystems
- ...and direct acyclic subnetworks
Tropical connections
Problem
For a given Kuramoto system with generic coefficients, what is the tropical variety it defines?
Weaker problem
For a given Kuramoto system with generic coefficients, what is the tropical stable intersection of this system?
Tropical semi-field
\[ \mathbb{T} = (\; \mathbb{R} \cup \{ \infty \} \;,\; \oplus \;,\; \odot \;) \] with \[ \begin{aligned} a \oplus b &= \min \,\{\, a\,,\, b\, \} & a \odot b &= a + b \end{aligned} \]
Tropical zero set
\[ \mathbb{V}( \text{Trop} (f)) \]
is the set of points where $\text{Trop}(f)$ is not differentiable.
Tropical stable intersection
For polynomials $f_1,\dots,f_n$, the limit set \[ \lim_{\epsilon \to 0} \bigcap_{i=1}^n [ \mathbb{V}(\text{Trop}(f_i)) + \epsilon \mathbf{v}_i ] \] for generic vectors $\mathbf{v}_1,\ldots,\mathbf{v}_n$ is well defined, and is called the stable intersection.
Given a Kuramoto system, can we compute the tropical stable intersection?
The dictionary
| Kuramoto network | Kuramoto equations | Adjacency polytope | Tropical intersection |
|---|---|---|---|
| Facet subnetworks | Facet subsystems | Facet | Stable intersection |
| Primitive subnetworks | Irreducible toric variety | Simplicial facet | Isolated intersection of multiplicity one |
Thank you!
- Chen arXiv:1703.01684 "Unmixing the mixed volume computation"
- Chen, Davis, Mehta arXiv:1708.09246 "Counting equilibria of the Kuramoto model using birationally invariant intersection index "
- Chen, Davis arXiv:1810.05690 "A toric deformation method for solving Kuramoto equations"
- Chen arXiv:1812.05408 "On the equality of BKK bound and birationally invariant intersection index"
- Chen arXiv:1903.04492 "Directed acyclic decomposition of Kuramoto equations"